CONTENT LIST
Trigonometry
The branch of mathematics that deals the properties of trigonometric functions and their application to the determination of the angles and sides of triangles.
Angle
When a ray AB starting from its initial position and rotates about its end point A and takes the final position AC, we say that an angle BAC (written as ∠ BAC) has been formed.
The amount of rotation from the initial side AB to the terminal side AC is termed as the measure of the angle.
Positive and Negative Angles
Positive Angles
An angle formed by a rotating ray is said to be positive if rotation is anticlock wise.
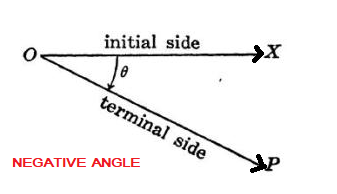
Negative Angles
An angle formed by a rotating ray is said to be negative if rotation is clock wise.
Measurement of Angles
There are three system for measuring angles,
- Sexagesimal System(Degree Measure)
- Centesimal System
- Circular System (Radian System)
Sexagesimal System(Degree Measure)
In Sexagesimal System, a right angle is divided into 90 equal parts,one part is known as degree. Symbol ° is used to expres degree.
One degree is divided into 60 equal parts, termed as minutes.Symbol ′ is used to expres minutes.
One minute is divided into 60 equal parts, termed as seconds. Symbols ″ are used to denote seconds.
Centesimal System
In Centesimal System, a right angle is divided into 90 equal parts, one part is known as grades.
One grades is divided into 100 equal parts, termed as minutes.Symbol ′ is used to expres minutes.
One minute is divided into 100 equal parts, termed as seconds. Symbols ″ are used to denote seconds.
Circular System (Radian System)
In this system, angle is measured in term of radian.
A radian is the angle subtended at the centre of a circle by an arc of equal length of radius of the circle.
Relation between radian and degree
π radian = 180°
Trigonometric Ratios
Trigonometric ratios or T-ratios express relation between different sides and angles of a right angled triangle.
There are six trigonometric ratios or T-ratios.These are sine (sin), cosine (cos), tangent (tan), cotangent (cot), cosecant (cosec), and secant (sec).
sine: Sine of an angle is the ratio of perpendicular to the hypotenuse.
cosine: Cosine of an angle the ratio of the base to the hypotenuse.
tangent: Tangent of an angle is the ratio of perpendicular to the
cosecant: Cosecant is a multiplicative inverse of sine.
secant: Secant is a multiplicative inverse of cosine.
cotangent: Cotangent is the multiplicative inverse of the tangent.
Quadrent
The x-axis and y-axis of a two-dimensional Cartesian plane system divide the plane into four regions called quadrants.
How to find value of trigometric function of any angle?
Step 1: Convert the given angle in term of (Nx90°+θ°)
Step 2:
Case A: If N= even number than there will no change in trigonmetric function .
Case B: If N= odd number than there will change in trigonmetric function .
- sin will change to cos .
- cos will change to sin .
- tan will change to cot .
- sec will change to cosec .
- cosec will change to sec .
- cot will change to tan .
Step 3: Idenify the quadrent of given angle and give sign +/- accordingly .
Example:1
Example:2
Test your understanding
a) (√3 – 1) / √2
b)(√3 – 1) / 2√2
c)(√3 – 1) / 2
d) None of these
Solution
sin15°= sin(45° – 30°) = (sin45° . cos30°) – (cos45° . sin30°)sin15° = (1/√2 . √3/2) – (1/√2 . ½)
sin15° = (√3 – 1) / 2√2
a) 1
b) cos56°
c) sin28°
d) None of these
Solution
We know that,cos(2A) = cos²A - sin²A
putting A=28°
cos²(28°)−sin²(28°)= cos56°
a) sin(10x)
b) 3sin²(10x)
c) 3sin(10x)
d) None of these
Solution
We know that,sin(2A) =2sinA.cosA
putting A=5x
6sin(5x)cos(5x)= 3sin(10x)
a) sin(34°)
b) cos²(34°)
c) cos(34°)
d) None of these
Solution
We know that,cos(2A) = 1 - 2sin²A
putting A=17°
1−2sin²(17°)=cos(34°)
Related Topics