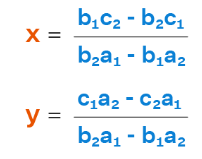Linear Equation in Two Variables Class 9

CONTENT LIST

Introduction

Some of the examples of linear equations are
2x – 3 = 0,
2y = 8,
m + 1 = 0,
x/2 = 3,
Above mentioned equations are examples of liner equations in one variable.Which you have studied in the previous class and the solution of each equation can be determined separately .
x + y = 2,
2x-y = 2,
x +3y = 12,
Above mentioned equations are examples of liner equations in two variable.Which you have studied in the class 9.Any linear equation in two variables has an infinite solution.To determine the unique solution of linear equations in two variables,We require a pair of linear equations .
An equation which can be written in the form ax + by + c = 0, where a, b and c are real numbers, and a and b are not both zero, is called a linear equation in two variables.

Graphical representation of Linear Equation in two Variable.

The graph of a linear equation is a straight line. Coordinates of each point on the line are a solution to the equation.The coordinates of a point represent the point's location on the Cartesian plane. Coordinates are written in ordered pairs:(x,y). Coordinate is also called ordered pair. A solution of linear equation in two variable involves a pair of values, one for x(first variable) and one for y(second variable) which satisfy the given equation.
Example: x+2y=0
When we take x=0, we get y=0, therefore (0,0)is the solution of the equation.
When we take x=4, we get y=–2, therefore (4,–2) is the solution of the equation.
When we take x=6 , we get y=–3 , therefore (6,–3) is the solution of the equation.
There is infinite solutions of a linear equation in two variables can be obtained as above.

When we draw a graph of ordered pair which is obtained as the solution of the above equation we get a straight line.

The polynomial having degree one is called a linear equation because its geometrical representation is a straight line.
x = 0 is the equation of the y - axis and y = 0 is the equation of the x - axis.
x = a is the equation of the straight line parallel to y - axis.
y = a is the equation of the straight line parallel to x - axis.

Finding the solution of a Linear Equation in Two Variables

The solution of a linear equation in two variables is determined using different methods, such as:

1. Substitution Method
2. Elimination Method
3. Graphical Method
4. Cross-multiplication Method

To determine the unique solution of linear equations in two variables,We require a pair of linear equations .

Substitution Method

Steps of solving lenar equation by Substitution Method

1. Solve one equation for either x or y.
2. Substitute the expression from step one into the 2nd equation.
3. Solve the second equation for the given variable as linear equation in one variable.
4. Put you solution back into the first equation and get value of another variable
5. Write your solution as a point.

Example: x - 5y = 7 and 2x - 4y = 8
Here equation 1 is 'x - 5y = 7'
x = 7 + 5y
Putting the value of 'x' in equation no.2
Equation2: 2x - 4y = 8
=> 2 * (7 + 5y) - 4y = 8
=> 14 + 10y - 4y = 8
=> 14 + 6y =8
=> 6y = 8 - 14
=> 6y = -6
=> y = -6/6
=> y = -1
The value of 'x' is :
x = 7 + 5y
=> 7 + 5 * -1
=> 7 + (-5)
=> 7 - 5
x = 2
∴ The root of the equation is (2,-1)

Elimination Method

Step 1: First of all, multiply both the given equations by some suitable non-zero constants to make the coefficients of any one of the variables (either x or y) numerically equal.
Step 2: After that, add or subtract equation-1 from the other in such a way that one variable gets eliminated. Thus, you get an equation in one variable, and determine the value of variable.
Step 3: Put this value of one varible obtained in any of the given equations to get the value of another variable.

Example: x - 5y = 7 and 2x - 4y = 8
x - 5y = 7 ------------------(equation i)
2x - 4y = 8 ------------------(equation ii)
Now multiply 2 in equation i and 1 in equation ii
2 * (x - 5y = 7) = 2x - 10y = 14------------------(equation iii)
1 * (2x - 4y = 8) = 2x - 4y = 8------------------(equation iv)
Now substract equation iii from equation iv
(2x - 4y) - (2x - 10y) = 8 - 14
2x - 4y - 2x - 10y = 8 - 14
4y - 10y = -6
6y = -6
y = -1
Putting the value of 'y' in equation i
x - 5y = 7
x - 5 * (-1) = 7
x - -5 = 7
x + 5 = 7
x = 7 - 5
x = 2
∴ The root of the equation is (2,-1)

Graphical Method

In order to determine solution of a pair of linear equations in two variables graphically we follow the below steps:
Step 1. Get the given pair linear equations in two variables.
Step 2. Plot the graph of the 1st equation and then the 2nd equation on the same coordinate system.
The following three cases may arise while plotting the graphs:
Case 1. If the graph lines of both the equation intersect at a point, then the given pair of linear equation has a unique solution and it is the coordinates of the point of intersection.
Case 2. If the graph lines are coinciding, then the system is consistent and has infinitely many solutions.
Case 3. If the graph lines are parallel, then the given system of equations is inconsistent that is it has no solution.
Now, let us solve the system of linear equations by the graphical method

Cross-multiplication Method

A given pair of linear equations in two variables:
(a)1x + (b)1y + (c)1 = 0
(a)2x + (b)2y + (c)2 = 0
By using cross multiplication, the values x and y will be:

How to determine solution of pair of linear equation would be unique, infinite many solution or no solution

A given pair of linear equations in two variables:
(a)1x + (b)1y + (c)1 = 0
(a)2x + (b)2y + (c)2 = 0

Test your understanding

Question:Which of the following is not a linear equation in two variables?
a) px + qy + c = 0
b) ax2 + bx + c = 0
c) 3x + 2y = 5
d) None of these

Answer:b) ax2 + bx + c = 0

Question:The degree of a linear equation is
a)1
b)2
c)3
d)0

Answer:b) a)1

Question:The graph of x = 5 is a straight line:
a) Intersecting both the axes
b) parallel to y-axis
c) parallel to x-axis
d) Passing through the origin

Answer:b) parallel to y-axis

Question: If (2, 0) is a solution of the linear equation 2x +3y = k, then the value of k is:
a) 4
b) 6
c) 5
d) 2

Answer: a) 4

Question: The graph of the linear equation 2x +3y = 6 cuts the y-axis at the point:
a) (2, 0)
b) (0, 3)
c) (3, 0)
d) (0, 2)

Answer: d) (0, 2)

Question: Any point on the line y = x is of the form:
a) (a, –a)
b) (0, a)
c) (a, 0)
d) (a, a)

Answer: d) (a, a)

Question: x = 9, y = 4 is a solution of the linear equation:
a) 2x + y = 17
b) x + y = 17
c) x + 2y = 17
d) 3x – 2y = 17

Answer: c) x + 2y = 17

Question: Any point on the x-axis is of the form:
a) (0, y)
b) (x, 0)
c) (x, x)
d) (x, y)

Answer: b) (x, 0)

Question:If a linear equation has solutions (–3, 3), (0, 0) and (3, –3), then it is of the form:
a)y – x = 0
b)x + y = 0
c) –2x + y = 0
d) –x + 2y = 0

Answer: b)x + y = 0

Question:The graph of the linear equation 5x + 3y = 10 is a line which meets the x-axis at the point:
a) (0, 3)
b) (3, 0)
c) (2, 0)
d) (0, 2)

Answer: c) (2, 0)

Question:The point of the form (a, –a) always lies on the line:
a) x = a
b) y = –a
c) y = x
d) x + y = 0

Answer: d) x + y = 0

Question: Equation of the line parallel to x-axis and 8 units above the origin is:
a) x = 8
b) x = –8
c)y = 8
d)y = –8

Answer: c) y = 8

Question: Through which of the following points, the graph of y = –x passes?
a) (1, 1)
b) (0, 1)
c) (–1, 1)
d) None of these

Answer: c) (–1, 1)

Question: On which of the following equations, the point of the form (m, –m) lies?
a) x = –m
b) x + y = 0
c) y = x
d) None of these

Answer: b) x + y = 0

Question: Which equation's graph is at a distance 3 units to the left of y-axis?
a) x = 3
b) x = –3
c) y = x
d) None of these

Answer: b) x = –3

Question: The graph of which of the following equations passes through the origin?
a) y = 2x + c
b) y = 2x – c
c) y = 2x
d) None of these

Answer: c) y = 2x

Question: How many linear equations in x and y can have a solution as (x = 1, y = 3)?
a) 1
b) 2
c) 3
d) infinite

Answer: d) infinite

Question: Write the linear equation whose solution is x = 1, y = 1.
a) x-y=0
b) x+y=0
c) 2x-y=0
d) x-2y=0

Answer: a) x-y=0

Question: Write the linear equation whose solution is x = 1, y = 1.
a) x-y=0
b) x+y=0
c) 2x-y=0
d) x-2y=0

Answer: a) x-y=0

Question: The linear equation 3x-11y=10 has:
a) Unique solution
b) Two solutions
c) Infinitely many solutions
d) No solutions

Answer: c) Infinitely many solutions

Question: The value of k, if x = 1, y = 2 is a solution of the equation 2x + 3y = k.
a) 5
b) 6
c) 7
d) 8

Answer: d) 8

Question: Point (3, 4) lies on the graph of the equation 3y = kx + 7. The value of k is:
a) 4/3
b) 5/3
c) 3
d) 7/3

Answer: b) 5/3

Question: The equation y = 5, in two variables, can be written as:
a) 1 .x + 1 .y = 5
b) 0 .x + 0 .y = 5
c) 1 .x + 0 .y = 5
d)0 .x + 1 .y = 5

Answer: d)0 .x + 1 .y = 5

Question: If x and y solutions for equation ax+by=c are negative and positive, the line lies in the:
a)First quadrant
b)Second quadrant
c)Third quadrant
d)Fourth quadrant

Answer: b)Second quadrant

Question: When the equation is multiplied or divided by a same non-zero number on both sides, the solution of the equation
a)Remains same
b)Increases
c)Changes when multiplied only
d)Changes when divided only

Answer: a)Remains same

Question: Find the number of solutions of the following pair of linear equations. x + 2y – 8 = 0 and 2x + 4y = 16:
a) 0
b) 1
c) 2
d) Infinite

Answer: d) Infinite

MCQ Test

Linear Equation In two Variable MCQ Test