CONTENT LIST
Lines
Line is a one-dimensional figure that extends in both directions infinitely .It has no width and height. It is made up by joining an infinite number of points close together.Euclid denotes the line as a breathless length.
Intersecting lines and Non intersecting lines
Intersecting lines are lines that cross one another.They have one point in common.
Non intersecting lines is also called paerallel line.Parallel lines are always same distance apart(This equal length is called the distance between two parallel lines), never cross each other, and do not have an endpoint in common.The edges of a ruler are parallel to each other.
Transversal Line
A transversal line intersects two lines at distinct points. In below figer t tranversal cut line l and m at two disdinct point p and O respectively.
Angle
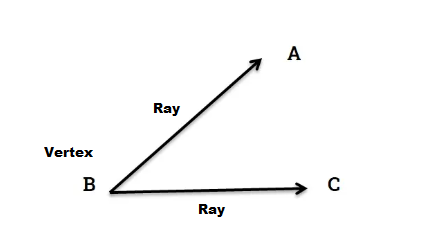
An angle is a shape that is formed by the intersection of two line segments, lines, or rays.
The two rays forming an angle are called the sides or arm of an angle, and the common endpoint is called the vertex.
The angle is represented using the symbol “∠”.
The measurement of angle between the two rays can be denoted using the Greek letter θ, α, β etc.
The angles are generally measured in degrees (°).
Based on the way of measurement of an angle from a line, It can be of two types of angles, such as a positive angle and a negative angle.
Positive & Negative angle
Negative Angle: If the angle is measured clockwise, then it is called a negative angle.
Interior of an angle & Exterior of an angle
The interior of ∠BAC is the set of all points in its plane which lie on the same side of AB as C and also on the same side of AC as B.
The exterior of ∠BAC is the set of all points in its plane which are not lie on the same side of AB as C and also on the same side of AC as B.
Types of Angles
The different types of angles are:
- Acute angle
- Right angle
- Obtuse angle
- Straight angle
- Reflex angle
- Full angle
- Complementary Angles
- Supplementary Angles
- Adjacent Angles
Acute Angle – an angle that has measure less than 90 degrees
Right Angle – an angle which is exactly at 90 degrees
Obtuse Angle – an angle that measure is greater than 90 degrees and less than 180 degrees
Straight Angle – an angle which is exactly at 180 degrees
Reflex Angle – an angle of measurement greater than 180 degrees and less than 360 degrees
Full Angle – an angle that measure is exactly at 360 degrees
Complementary Angles
Two angles having a sum of 90 degrees are called complementary angles.
Supplementary Angles
Two angles are said to be supplementary angles sum of measure of angles180 degrees.
Adjacent Angles
Two or more angles that have a common vertex and common one side are known adjacent angles.
Linear Pair Angles
Two angles are said to be linear pair if they have one arm common & the sum of adjecent angle is 180 degree
Linear pair axiom:
If a ray stands on a line, then the sum of the two adjacent angles so formed is 180° and viceversa.
Vertically opposite angle
When two straight lines intersect on a point then two pairs of verically opposite angle is formed
Theorem: If two lines intersect each other, then the vertically opposite angles are equal.
Transversal and Parallel Lines
In below figer EF and GH are two parallel lines and a transversal RS cuts parallel lines at two point M and N respectively.
